FLUX-SURFACE GEOMETRY

Clebsch coordinates

GYRO/CGYRO/NEO use a right-handed (positively-oriented), field-aligned coordinate system \((r,\theta,\alpha)\) and the Clebsch field representation [KK58]

\[\mathbf{B} = \nabla\alpha\times\nabla\psi \quad \text{such that} \quad\mathbf{B}\cdot\nabla\alpha = \mathbf{B}\cdot\nabla\psi = 0\]

where \(\psi\) is the poloidal flux divided by \(2\pi\) and

\[\alpha =\varphi +\nu (r,\theta)\]

is the Clebsch angle. Here, \(\varphi\) is the toroidal angle, oriented as shown in the figure below, and \(\theta\) is the poloidal angle which increases as one moves counterclockwise along the flux-surface (shown in blue). In these coordinates, the Jacobian is

\[{\mathcal J}_\psi \doteq \frac{1}{\nabla\psi\times\nabla\theta\cdot\nabla\alpha} = \frac{1}{\nabla\psi\times\nabla\theta\cdot\nabla\varphi} \; .\]

Since the coordinates \((\psi,\theta,\alpha)\) and \((\psi,\theta,\varphi)\) form right-handed systems, the Jacobian \({\mathcal J}_\psi\) is positive-definite. In the latter coordinates, the magnetic field becomes

\[\mathbf{B} = \nabla\varphi\times\nabla\psi + \frac{\partial \nu}{\partial \theta} \nabla\theta\times\nabla\psi\]

Using the definition of the safety factor, \(q(\psi)\), we may deduce

\[q(\psi) \doteq \frac{1}{2\pi} \int_0^{2\pi} \frac{\mathbf{B}\cdot\nabla\varphi}{\mathbf{B}\cdot\nabla\theta} \, d\theta = \frac{1}{2\pi} \int_0^{2\pi} \left( -\frac{\partial \nu}{\partial \theta} \right) \, d\theta = \frac{\nu(\psi,0)-\nu(\psi,2\pi)}{2\pi} \; .\]

\[\]

For concreteness, we choose the following boundary conditions for \(\nu\):

\[\begin{split}\nu(\psi,2\pi) = &~-2\pi \, q(\psi) \; , \\ \nu(\psi,0) = &~0 \; .\end{split}\]

By writing \(\mathbf{B}\) in the standard form

\[\mathbf{B} = \nabla\varphi\times\nabla\psi + I(\psi) \nabla\varphi \; ,\]

we can derive the following integral for \(\nu\):

\[\nu(\psi,\theta) = -I(\psi)\int_0^\theta {\mathcal J}_\psi \left|\nabla\varphi\right|^2 d\theta\; .\]

In the case of concentric (unshifted) circular flux surfaces, one will obtain the approximate result \(\nu(\psi,\theta) \sim -q(\psi)\theta\). Finally, we remark that the coordinate systems \((R,Z,\varphi)\) and \((r,\theta,\varphi)\) are positively oriented.

Bounding-box method

In the MXH parameterization [ACB20], we use the bounding-box method to define

• minor radius \(r\)

• major radius \(R_0\)

• elongation \(\kappa\)

• elevation \(Z_0\)

via the flux-surface contour extrema

\[\begin{split}2 r = & \max_\ell(R) - \min_\ell(R) \; , \\ 2 \kappa r = & \max_\ell(Z) - \min_\ell(Z) \; , \\ 2 R_0 = & \max_\ell(R) + \min_\ell(R) \; , \\ 2 Z_0 = & \max_\ell(Z) + \min_\ell(Z) \; .\end{split}\]

Effective field

The effective field strength, \(B_{\rm {unit}}\), is defined as

\[B_\mathrm{unit} = \frac{1}{r} \frac{d\chi _{t}}{dr} \; ,\]

where \(\chi _{t}\) is the toroidal flux divided by \(2\pi\). This gives the roughly equivalent field that would be obtained if the flux surface was deformed to a circle.

Equilibria

GYRO/CGYRO/NEO can be run using circular equilibrium or shaped Grad-Shafranov equilibrium.

(1) Circular equilibrium

The flux surfaces, which are not local G-S equilibria, have the form:

\[\begin{split}R(r,\theta) &= R_0 + r \cos \theta \\ Z(r,\theta) &= r \sin \theta \\\end{split}\]

where \(\nu(r,\theta) = -q(r) \theta\).

• CGYRO: EQUILIBRIUM_MODEL = 1

• NEO: EQUILIBRIUM_MODEL = 0

(2) Shaped Grad-Shafranov equilibrium

The flux surfaces, which are local G-S equilibria, have the new MXH3 parameterization [ACB20]:

\[\begin{split}R(r,\theta) &= R_0(r) + r \cos \theta_R \\ Z(r,\theta) &= Z_0(r) + \kappa(r) r \sin \theta\end{split}\]

where \(\nu(r,\theta)\) is computed numerically. The harmonic angle \(\theta_R\) is

\[\theta_R = \theta + c_0(r) + \sum_{n=1}^{3} \left[ c_n(r) \cos n \theta + s_n(r) \sin n \theta \right]\]

• \(c_n\) are anti-symmetric moments and \(s_n\) are symmetric moments.

• CGYRO: EQUILIBRIUM_MODEL = 2

• NEO: EQUILIBRIUM_MODEL = 2 or PROFILE_EQUILIBRIUM_MODEL = 1

• For experimental profiles, shape parameters are auto-generated from profile data.

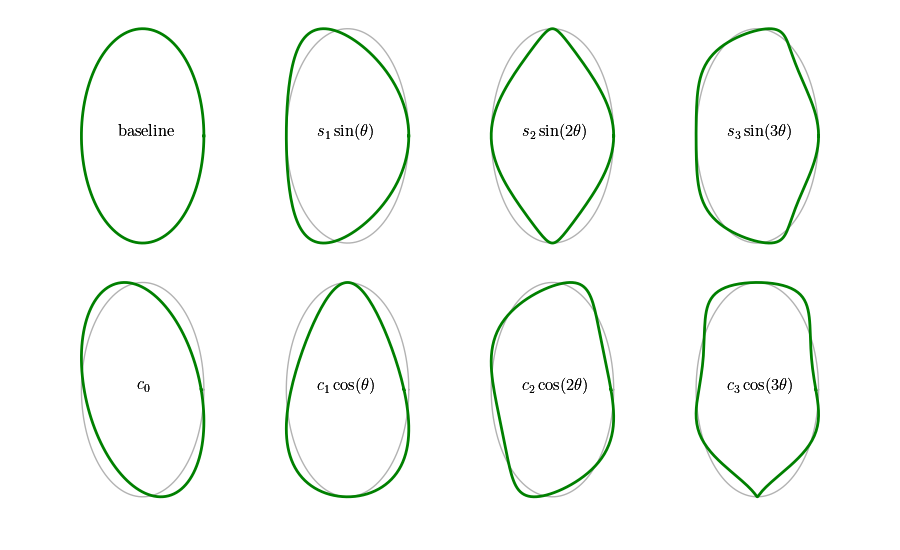
Table of geometry parameters

Symbol	input.cgyro parameter	input.neo parameter	meaning
\(r/a\)	RMIN	RMIN_OVER_A	minor radius
\(R_0(r)/a\)	RMAJ	RMAJ_OVER_A	major radius
\(\partial R_0/\partial r\)	SHIFT	SHIFT	Shafranov shift
\(Z_0(r)/a\)	ZMAG	ZMAG_OVER_A	elevation
\(\partial Z_0/\partial r\)	DZMAG	S_ZMAG	elevation shift
\(q\)	Q	Q	safety factor
\(s\)	S	SHEAR	shear
\(\kappa\)	KAPPA	KAPPA	elongation
\(s_\kappa\)	S_KAPPA	S_KAPPA
\(\delta = \sin s_1\)	DELTA	DELTA	triangularity
\(s_\delta\)	S_DELTA	S_DELTA
\(\zeta = -s_2\)	ZETA	ZETA	squareness
\(s_\zeta\)	S_ZETA	S_ZETA
\(c_0\)	SHAPE_COS0	SHAPE_COS0	tilt
\(s_{c_0}\)	SHAPE_S_COS0	SHAPE_S_COS0
\(c_1\)	SHAPE_COS1	SHAPE_COS1	ovality
\(s_{c_1}\)	SHAPE_S_COS1	SHAPE_S_COS1
\(c_2\)	SHAPE_COS2	SHAPE_COS2
\(s_{c_2}\)	SHAPE_S_COS2	SHAPE_S_COS2
\(c_3\)	SHAPE_COS3	SHAPE_COS3
\(s_{c_3}\)	SHAPE_S_COS3	SHAPE_S_COS3
\(s_3\)	SHAPE_SIN3	SHAPE_SIN3
\(s_{s_3}\)	SHAPE_S_SIN3	SHAPE_S_SIN3
\(\beta_e\)	BETAE_UNIT	NA
\(\beta_*\) scaling	BETA_STAR_SCALE	BETA_STAR
BTCCW	BTCCW	BTCCW
IPCCW	IPCCW	IPCCW

For further information about geometry and normalization conventions, consult the GYRO Technical Guide [CB10].

Magnetic field orientation

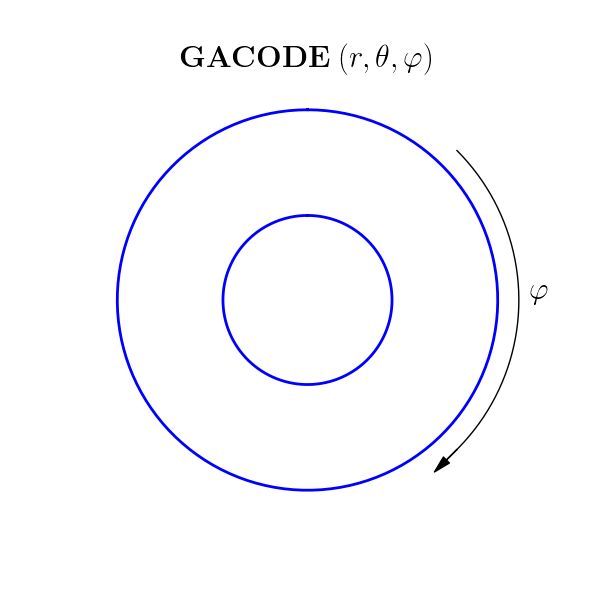
GACODE uses a right-handed (positively-oriented), field-aligned coordinate system \((r,\theta,\varphi)\), whereas DIII-D uses a (positively-oriented) cylindrical system \((R,\phi,Z)\). Looking down on the tokamak from above, the orientation of the GACODE toroidal angle is clockwise, whereas the DIII-D toroidal angle is counter-clockwise:

In reality, quantities like the safety factor and poloidal flux have definite signs. Historically, these signs have been suppressed or neglected in both theory and modeling. For proper treatment of momentum transport, however, these signs must be retained. We can infer typically neglected signs by knowing IPCCW and BTCCW. For example:

• sign(\(B_{\rm tor}\)) = -BTCCW

• sign(\(B_{\rm pol}\)) = -IPCCW

• sign(\(\psi_{\rm pol}\)) = -IPCCW

• sign(\(q\)) = IPCCW \(\times\) BTCCW

The standard configuration in DIII-D is shown below.

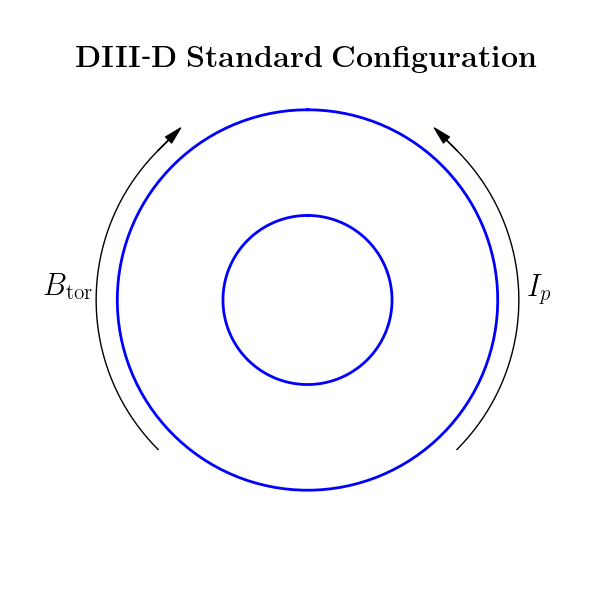
This corresponds to IPCCW = 1 and BTCCW =-1. Thus, in GACODE coordinates, we expect:

• sign(\(B_{\rm tor}\)) = 1

• sign(\(B_{\rm pol}\)) = -1

• sign(\(\psi_{\rm pol}\)) = -1

• sign(\(q\)) = -1

In other words, the safety factor and poloidal flux are negative in the typical case. This will be reflected in a properly-constructed input.gacode file.

Toroidal and poloidal flux

We can start from the general forms of the toroidal and poloidal fluxes [DHCS91]

\[\begin{split}\Psi_t \doteq &~\iint\limits_{S_t} \mathbf{B} \cdot d{\bf S} = \frac{1}{2\pi} \iiint\limits_{V_t} \mathbf{B} \cdot \nabla\varphi \, dV \; , \\ \Psi_p \doteq &~\iint\limits_{S_p} \mathbf{B} \cdot d{\bf S} = \frac{1}{2\pi} \iiint\limits_{V_p} \mathbf{B} \cdot \nabla\theta \, dV \; .\end{split}\]

Explicitly inserting the field-aligned coordinate system of the previous section, and differentiating these with respect to \(\psi\), gives

\[\begin{split}\frac{d\Psi_t}{d\psi} = &~\frac{1}{2\pi} \int_0^{2\pi} d\varphi \int_0^{2\pi} d\theta \,\, \mathbf{B}\cdot\nabla\varphi \, {\mathcal J}_\psi \; , \\ = &~\frac{1}{2\pi} \int_0^{2\pi} d\varphi \int_0^{2\pi} d\theta \,\, \frac{\mathbf{B}\cdot\nabla\varphi}{\mathbf{B}\cdot\nabla\theta} \; , \\ = &~2 \pi \, q(\psi) \; ,\end{split}\]

\[\begin{split}\frac{d\Psi_p}{d\psi} = &~\frac{1}{2\pi} \int_0^{2\pi} d\varphi \int_0^{2\pi} d\theta \,\, \mathbf{B}\cdot\nabla\theta \, {\mathcal J}_\psi \; , \\ = &~\frac{1}{2\pi} \int_0^{2\pi} d\varphi \int_0^{2\pi} d\theta \; , \\ = &~2 \pi \; .\end{split}\]

Thus, \(\psi\) is the poloidal flux divided by \(2\pi\). For this reason, it is useful to also define the toroidal flux divided by \(2\pi\):

\[\chi_t \doteq \frac{1}{2\pi} \Psi_t\; .\]

According to these conventions,

\[d\Psi_t = q \, d\Psi_p \quad \mbox{and} \quad d\chi_t = q \, d\psi \; .\]